By Group "Snapshot", written by Patrick van Ewijk

Dear readers, this is a blog post about our model. Although I'm curious to start immediately with the problems we encountered in python, first I refer to an external document which I wrote (see: model.pdf). It contains the explanation of our model. As it includes a lot of mathematical symbols however, we decided not to publish it here in this blog post.

Very short explanation of model

We impose a form where the difference of the log-prices (which is considered as the return of that period), follows a Normal distribution with a mean mu and standard deviation sigma. Sigma squared contains the same regressors as the GARCH(1,1) model (a constant, the previous period return squared and the previous sigma squared) and some external regressors (captured in X). The idea is to compare "our" model with the GARCH(1,1) model.

Initial model in python

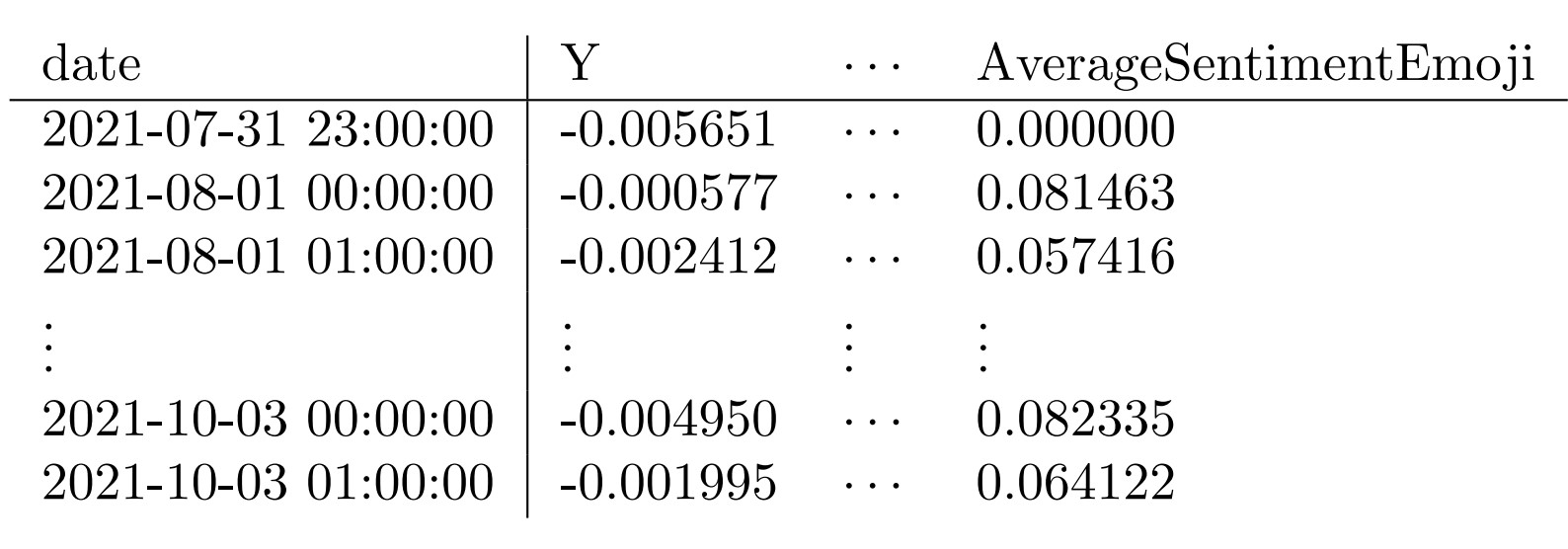
Structure of dataframe

For fitting the model, a dataframe is used consisting of gathered information from the tweets. It is chronologically ordered. Whenever ones want to verify the results in this blog post, one needs to download the dataframe (see link: btc_info_df.pickle). As an illustration, we present a visualization of the structure of the dataframe.

Functions specifying negative log-likelihood and sigma

For the fitting of the model, we need to maximize the log-likelihood function. This is equivalent to minimizing the negative of the log-likelihood function. We use the minimize module from scipy.optimize. Further, we need pandas for a dataframe operation and numpy in our log-likelihood function.

from scipy.optimize import minimize
import pandas as pd
import numpy as np

We made the following code for the forms of sigma and the negative likelihood. The mu vector is simply the average of the y_vec terms. Hence, it does not depend upon the parameters in the sigma function and we exclude it from the parameters which we are still estimating in the likelihood function. The function is flexible in the sense that it allows us to estimate GARCH(1,1) easily as well. If we only input a vector of parameters of length 3, the GARCH(1,1) model is estimated.

def sigma_sqf(param,X, y_vec,mu): 
    omega=param[0]
    alpha_1=param[1]
    beta_1=param[2]
    if len(param)>=4:
        gamma_v=param[3:]
    else:
        gamma_v=np.repeat(0, X.shape[1])
    sigma_sq=np.repeat((y_vec[0]-mu)**2,len(y_vec)) 
    for i in range(2,len(y_vec)):
        sigma_sq[i]=\
            omega+alpha_1*(y_vec[i-1]-mu)**2+\
            beta_1*sigma_sq[i-1]+np.dot(X[i-1,], gamma_v)
    sigma_sq=sigma_sq[1:]
    return sigma_sq

def Adj_Neg_Log_likelihood(param, X, y_vec, mu):
    sigma_sq=sigma_sqf(param, X,y_vec, mu)
    return 0.5*np.sum(np.log(sigma_sq))+\
        0.5*np.sum((y_vec[1:]-mu)**2/sigma_sq)

One might wonder where the (y_vec[0]-mu)**2 comes from. Note that the first sigma squared cannot be estimated according to the model. Therefore this is simply set to the squared deviation of the previous day return from the mean of the returns.

The goal is to minimize Adj_Neg_Log_likelihood, as a function of param. The other parameters X, y_vec and mu are known before we start minimizing the function.

Initializing of minimize function

minimize takes several arguments. First of all, we need to come up with an initial guess x0. Further we specify method. As Adj_Neg_Log_likelihood is non-linear, method=SLSQP is chosen. Besides, we have some fixed arguments for the function (that is: X, y_vec and mu). We retrieve the desired columns of our dataframe btc_info_df in X, which can be considered as a matrix instead of a dataframe. Finally, we specify options. Here 'eps' is a pre-fixed parameter which determines how precise the slope of Adj_Neg_Log_likelihood in param will be estimated.

x0_1=np.array([0.0004,0.06,0.93,0.0000,0.0000, 0.0, 0.0])
method='SLSQP'
X=pd.DataFrame(btc_info_df[['PercSentiment_.95',\
    'PercSentiment_.05', 'AverageSentiment',\
    'AverageSentimentEmoji']]).to_numpy()
arguments= (X,btc_info_df.Y,np.average(btc_info_df.Y),)
options={'eps' : 1e-6}

Minimizing process

Now, the minimize function is called.

minimize(Adj_Neg_Log_likelihood, x0=x0_1, method=method,\
    options=options, constraints=nonlinconst,\
    args=arguments)

Problems in function

Problem 1: Different x0, different minima

When we tried different initial guesses for x0, we found out that different choices of x0 lead to different minima of Adj_Neg_Log_likelihood. Our first thought was that minimize found a local minima, instead of a global one.

Problem 2: Infeasible solutions

Sigma squared is a variance and needs to be greater or equal to zero. However, during the minimization process sometimes allocations of param were tried for which sigma squared is negative. This led to infeasible solutions.

Improving our code

Problem 2 was solved by adding a constraint on sigma_sqf such that it cannot be negative. That is, we created nonlinconst and added this as an argument to minimize:

nonlinconst= {'type': 'ineq', 'fun':sigma_sqf, 'args':arguments}
minimize(Adj_Neg_Log_likelihood, x0=start_guess, method=method,\
    options= options, constraints=nonlinconst,\
        args=arguments)

Problem 1 was more difficult. At some moment I found an answer to the problem (link to solution: stackoverflow). It turned out that minimize works better if we work with larger numbers. As long as we are consistent with this, multiplying our y_vec is not a problem. By trial and error a scale factor of 250 worked.

X=pd.DataFrame(btc_info_df[['PercSentiment_.95', \
    'PercSentiment_.05', 'AverageSentiment', 'AverageSentimentEmoji']]).to_numpy()
scale=250
arguments= (X,btc_info_df.Y*scale,np.average(btc_info_df.Y)*scale,)
nonlinconst= {'type': 'ineq', 'fun':sigma_sqf, 'args':arguments }

x0_1=np.array([0.0004,0.06,0.93,0.0000,0.0000, 0.0, 0.0])
x0_2=np.array([0.004,0.009,0.80,0.004 , - 0.00002, -0.000004, 0.0005])
x0_3=np.array([0.9,0.1,0.8,0.044 , 0.000005, 0.00000099, 0.00000022])
x0_4= np.array([2.14545724e-04,  6.00103308e-02,  9.30000766e-01,\
    1.21472916e-04, 1.28891903e-04, -3.42864190e-05, -1.18436185e-05])

print("Values of our model:")
startingvalues=[x0_1,x0_2,x0_3,x0_4]
for start_guess in startingvalues:
    resExo=\
        minimize(Adj_Neg_Log_likelihood, x0=start_guess, method='SLSQP',\
            options= options, constraints=nonlinconst,\
                args=arguments)
    print(resExo.fun)

For every initial guess, we now obtain the same value of Adj_Neg_Log_likelihood (1596.8731).

Comparison with GARCH(1,1)

As explained earlier, whenever we input a vector param of length 3 in Adj_Neg_Log_likelihood, automatically Adj_Neg_Log_likelihood sees that we mean the GARCH(1,1) model. Thus, fitting the GARCH(1,1) model is quite easy. We only need to drop parameters 4 up to 7 of the initial guesses x0. This leads to the following code.

print("Garch values:")
x0_1g=np.array([0.0004,0.06,0.93])
x0_2g=np.array([0.004,0.009,0.80])
x0_3g=np.array([0.9,0.1,0.8])
x0_4g= np.array([2.14545724e-04,  6.00103308e-02,  9.30000766e-01])
startingvalues=[x0_1g,x0_2g,x0_3g,x0_4g]
for start_guess in startingvalues:
    Garch=\
        minimize(Adj_Neg_Log_likelihood,x0=start_guess, method='SLSQP',\
        options= options, constraints=nonlinconst, args=arguments)
    print(Garch.fun)

We find a value of Adj_Neg_Log_likelihood of 1602.0816. Note that its not weird our model fits better than GARCH(1,1), as it includes additional parameters. Indeed we see that -1596.8731>-1602.0816.

However, one could test if it is significantly better by doing a likelihood ratio test. Under the null hypothesis that the GARCH(1,1) is not worse than our model, 2 times the difference in log-likelihoods should follow a chi squared distribution with 4 degrees of freedom.

The test statistic 10.417 and as the critical value is 9.488, we reject the null hypothesis that the data follows GARCH(1,1) over our model. In other words, indeed the sentiment regressors help to estimate the volatility in a better way.

Final Possible Steps in model

• Drop the constraint sigma_sqf>0. Instead, we will square the elements in X or replaces the linear function X_{t-1}'gamma by exp(X_{t-1}'gamma) (see external document section 1.4). Note that in the first case, we still need to put a bound on gamma (if the algorithm tries gamma <0, sigma_sqf could still be negative).

• If time allows, look into a completely different model.