By Group "Python at large"
This post describes how we utilize textual analysis techniques to measure the readability of the extracted pieces of MD&A from 10-k files, with mainly three different approaches: the fog index, the common words ratio, and the vocabulary ratio, all of which are commonly seen in relevant academic studies. We follow the definition of each approach described in Measuring Readability in Financial Disclosures (Loughran and Mcdonald, 2014).
The Fog index
The Fog index is definied as a linear combination of average words per sentence and the percentage of complex words (depending on how many syllables a word has). To calculate these two components, we use nltk.sent_tokenize and nltk.word_tokenize to find the number of sentences and words, before converting them to the number of words per sentence. Then we apply SyllableTokenizer() on the tokenized words which would convert the word list to a list of the number of syllables, allowing us to count the number of words with certain conditions on syllables that we specify. Besides following the definition of complex words in Loughran and Mcdonald (2014) as having more than two syllables, we increase the threhold to more than three syllables, allowing for sensitivity tests in the regressions. The details can be found in the notes of the following code.
def number_of_sentence(txt):
txt = re.sub("^\d+", " ", txt) # delete digs
sentence_list = nltk.sent_tokenize(txt)
return len(sentence_list)
''' The number of words after removing the punctuation and digits '''
def total_number_of_words(txt):
txt = re.sub(r'[^\w\s]', '', txt)
txt = re.sub("^\d+", " ", txt)
tokenized_word = word_tokenize(txt)
return len(tokenized_word)
''' The number of words after removing the punctuation, digits and the stop words | For more reasonable computation of fog index '''
def total_number_of_words_netstopping(txt):
txt = re.sub(r'[^\w\s]', '', txt.lower().strip())
txt = re.sub("^\d+", " ", txt)
tokenized_word = word_tokenize(txt)
stop_words = set(stopwords.words("english"))
filtered_word = []
for w in tokenized_word:
if w not in stop_words:
filtered_word.append(w)
return(len(filtered_word))
''' Complex Words - more than two syllables; More Complex Words - more than three syllables'''
def number_of_complex_words(txt):
SSP = SyllableTokenizer()
txt = re.sub(r'[^\w\s]', '', txt.lower().strip())
txt = re.sub("^\d+", " ", txt)
word_list = nltk.word_tokenize(txt)
syllable_list = []
for word in word_list:
syllable_list.append(len(SSP.tokenize(word)))
count2 = len([elem for elem in syllable_list if elem > 2]) # Based on the standard definition of fog index
count3 = len([elem for elem in syllable_list if elem > 3]) # Another threshold in case of insensitivity
return count2,count3
Now that we have the functions to obtain the main components, it’s convenient to compute the fog index and store in our mda file.
if __name__ == '__main__':
mda = pd.read_csv("./mda.csv")
for i in range(0, 1497): #1497 is the no. of our sample
mda["mda_length"][i] = len(mda["mda"][i])
mda["number_of_sentence"][i] = number_of_sentence(mda["mda"][i])
mda["average_words_per_sentence"][i] = total_number_of_words(mda["mda"][i])/mda["number_of_sentence"][i]
(count2, count3) = number_of_complex_words(mda["mda"][i])
mda["number_of_complex_words"][i] = count2
mda["number_of_more_complex_words"][i] = count3
'''Percentage of complex words with slightly different specifications'''
mda["percent_of_complex_words_100"][i] = 100 * (mda["number_of_complex_words"][i]/total_number_of_words(mda["mda"][i]))
mda["percent_of_more_complex_words_100"][i] = 100 * (mda["number_of_more_complex_words"][i] / total_number_of_words(mda["mda"][i])):
mda["percent_of_complex_words_100_net"][i]=100 * (mda["number_of_complex_words"][i] /total_number_of_words_netstopping(mda["mda"][i]))
mda["percent_of_more_complex_words_100_net"][i] = 100 * (mda["number_of_more_complex_words"][i] / total_number_of_words_netstopping(mda["mda"][i]))
'''Fog index with four slightly different specifications'''
mda["fog_index_a"][i]= 0.4 * (mda["percent_of_complex_words_100"][i]+mda["average_words_per_sentence"][i])
mda["fog_index_ma"][i] = 0.4 * (mda["percent_of_more_complex_words_100"][i] + mda["average_words_per_sentence"][i])
mda["fog_index_s"][i]= 0.4 * (mda["percent_of_complex_words_100_net"][i]+mda["average_words_per_sentence"][i])
mda["fog_index_ms"][i] = 0.4 * (mda["percent_of_more_complex_words_100_net"][i] + mda["average_words_per_sentence"][i])
mda.to_csv("./fogindex_mda.csv")

Note: Although the Fog index is one of the widely used measurements for readability, it is faced with as wide criticism when applied in finance-related documents. One of the most serious concerns is that its definition of complex words by syllables appears to be unsensitive in business documenet(Loughran and Mcdonald, 2014). Polysyllabic words like “company”, “financial”, “department”, and “generate”, to name a few, are heavily used in financial files and make perfect sense to people in business. However, they are all classified as complex words by the standard definition of fog index since they have more than two syllables. We try to ease this issue in our project by increasing the threshold. But the intrinsic problem may still persists.
Common words ratio
This method (also the Vocabulary index ) takes a whole new approach of measuring readability - not by the absolute complexity of sentences and words but by the relative rareness of the vocabulary in a piece of text. In Loughran and Mcdonald(2014)'s research, the authors use an external master dictionary to check if words are matched with a valid meaning. However, such external dictionary is not avaliable to us. We Instead begin with building our own dictionary as a vocabulary list of all the MD&A files considered together(after the removal of the punctuation and digits, and lemmatization using function WordNetLemmatizer). Then for each word in the vocabulary list, we compute its ratio of appearance in all the files as a measurement of its rareness. The ratio could take a value from 0 to 1. For instance, ratio = 1 indicates that the word is can be found in all the files, such as “financial” and “revenue”. And ratio = 0.1 indicates the word can be found in 10% of the files. Lastly, we iterate every (lematized) words in one file and measure the file's readability as the average ratio.
'''Function for building a dictionary of all the text files'''
def txt_to_wordlist(txt):
txt = re.sub(r'[^\w\s]', '', txt.lower().strip())
txt = re.sub(" \d+", " ", txt)
tokenized_word = word_tokenize(txt)
tokenized_word = set(tokenized_word)
tokenized_word = list(tokenized_word)
lem = WordNetLemmatizer()
lem_words = []
for w in tokenized_word:
lem_words.append(lem.lemmatize(w, "v"))
return list(set(lem_words))
def split_dataframe(df, chunk_size = 4000):
chunks = list()
num_chunks = math.ceil(len(df) / chunk_size)
for i in range(num_chunks):
chunks.append(df[i*chunk_size:(i+1)*chunk_size])
return chunks
def txt_to_wordlist_duplicate(txt):
txt = re.sub(r'[^\w\s]', '', txt.lower().strip())
txt = re.sub(" \d+", " ", txt)
tokenized_word = word_tokenize(txt)
lem = WordNetLemmatizer()
lem_words = []
for w in tokenized_word:
lem_words.append(lem.lemmatize(w, "v"))
return list(set(lem_words))
''' Iteration for dictionary begins'''
if __name__ == '__main__':
fog = pd.read_csv(r"./Extraction.csv")
del fog["Unnamed: 0"]
fog = fog.dropna()
#make a word relative frequency
#get a string with all item_7
all_mda = '.'.join(fog["mda"])
#get a word list with all words in it
all_word_list = txt_to_wordlist(all_mda)
# build a 2-dimension list[[wordlist1],[wl2],[wl3],...]
item_7 = fog["mda"].to_list()
two_d_list = []
for item in item_7:
two_d_list.append(txt_to_wordlist(item))
count = 0
words_common_show_time = []
for word in all_word_list:
counter = 0
for word_list in two_d_list:
if word in word_list:
counter += 1
else:
pass
words_common_show_time.append(counter)
count += 1
print(100 * count / len(all_word_list))
words_common_ratio = []
for i in words_common_show_time:
words_common_ratio.append(i / len(two_d_list))
print("Complete!")
#get word_ratio_dictionary
word_ratio_dictionary = dict(zip(all_word_list, words_common_ratio))
df = pd.DataFrame(word_ratio_dictionary.items(), columns=['Words', 'common_ratio'])
df.to_csv("Commonwords_Dictionary.csv")
print("Dictionary saved!")
'''Compute the rareness score of each text file'''
if __name__ == '__main__':
#Create another 2d list with wordlist in which the words will duplicate
two_d_list_dup = []
for item in item_7:
two_d_list_dup.append(txt_to_wordlist_duplicate(item))
common_words_ratio_list = []
for wordlist in two_d_list_dup:
common_words_ratio = 0
for word in wordlist:
try:
common_words_ratio = common_words_ratio + word_ratio_dictionary[word]
except KeyError:
common_words_ratio = common_words_ratio + 0
common_words_ratio_list.append(common_words_ratio/len(wordlist))
fog["common_words_ratio_list"] = common_words_ratio_list
fog.to_csv("independent_variable(lem_with_frequency).csv")
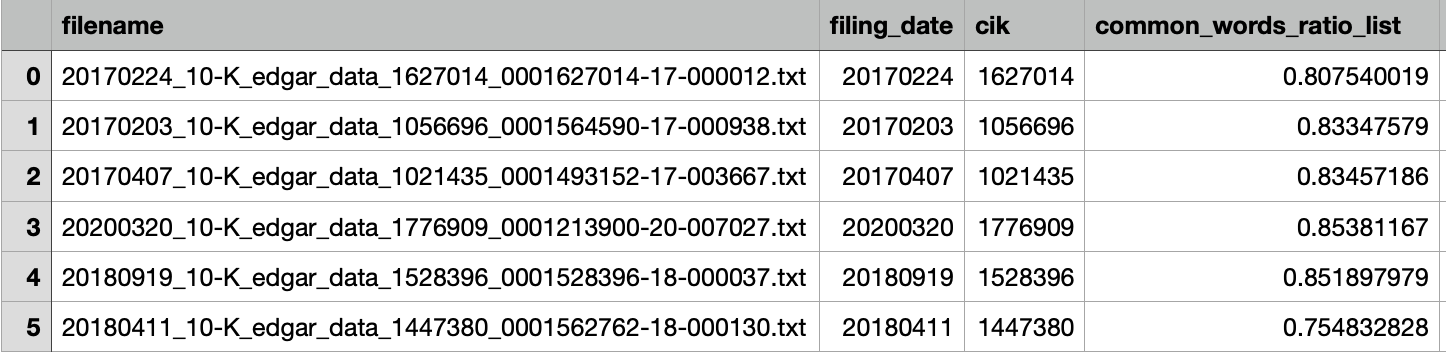
Note: One of the our biggest concerns of this method is its dominance by the large portion of overlapping words across documents as all MD&A files follow a general and standard format. One could already observe from the sample ratio we provided above that the results are generally above 0.8 and the differences are sometimes as small as 1-2%. We are thus quite worried about its sensitivity to rare words as the small differences in rare words could be absorbed by the variation across companies.
Vocabulary approach
This approach shares the spirit with the common words approach we described above, measuring the readability of a piece of text by the rareness of its vocabulary. Similar to the last method, we begin by creating a volcabulary list of all the unique words among the sample files. Then, we calculate the volcabulary that a piece of text use as a portion of all the volcabulary in the dictionary to be the indicator of complexity. A higher ratio indicates that the files consist of more vocabulary and are perceived to be less readable.
This method could be easily attained using the union and intersection function of the set. As always, we clean the punctuation and digits before tokenizing the words. We then update the vocabulary set with the union function. To compute the vocabulary used in every piece of text, we use the intersect function and compute the length of the intersection.
vol = set()
'''Build a grand dictionary'''
for i in range(0, 1497):
text = mda["mda"][i]
text = re.sub(" \d+", " ", text) # Clear all the numbers
text_word = word_tokenize(text)
lem_words = []
for w in text_word:
lem_words.append(wnl.lemmatize(w, "v"))
text_vol = set(lem_words)
vol = vol.union(text_vol)
print(i)
'''Compute the volcabulary used in each file'''
for i in range(0, 1497):
text = mda["mda"][i]
text = re.sub(r'[^\w\s]', '', text.lower().strip())
text = re.sub(" \d+", " ", text)
text_word = word_tokenize(text)
lem_words = []
for w in text_word:
lem_words.append(wnl.lemmatize(w, "v"))
text_vol = set(lem_words)
mda["vocabulary"][i] = len(text_vol.intersection(vol))
mda["ratio_in_vol"][i] = len(text_vol.intersection(vol))/len(vol)
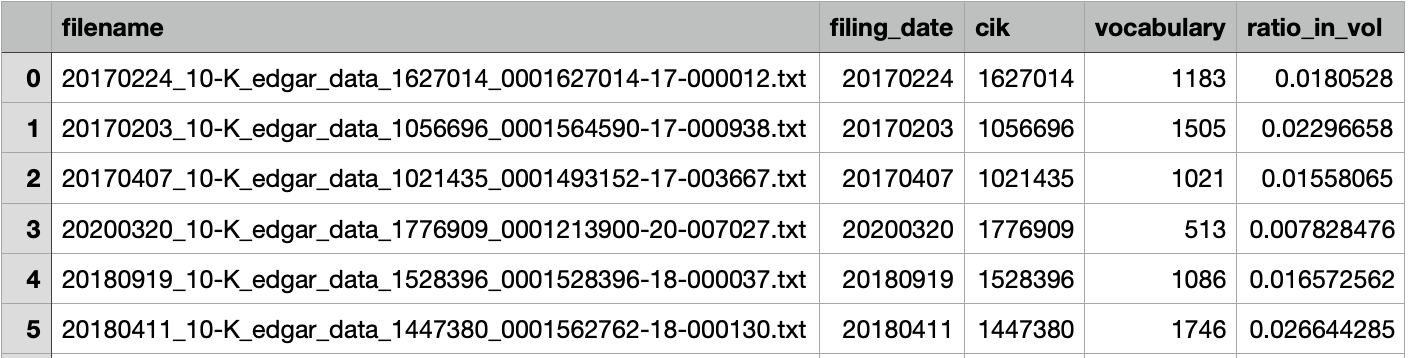
Note: The original vocabulary method used in the literature (Loughran and Mcdonald, 2014) is to match every word in the text file with an external financial dictionary. However, such a dictionary is patent-protected and not available to our project. We thus make a compromise by building our small dictionary with the samples at hand. Surely our method is not as favorable as matching an external financial dictionary since the latter could filter the financial terminologies in the files, allowing the measurement to be less sensitive to the use of common words. In addition, it’s not very obvious why more vocabulary will lead to less readability.